자바스크립트 기초 강의에서 배운 메소드들
- push(): 뒤에 삽입
- pop(): 뒤에 삭제
- unshift(): 앞에 삽입
- shift(): 앞에 삭제
arr.splice(n, m): n부터 m개의 요소를 지움
- 삭제된 요소 반환
let arr = [1, 2, 3, 4, 5];
let result = arr.splice(1, 2);
console.log(arr); //[1, 4, 5]
console.log(result); //[2, 3]
arr.splice(n, m, x): n부터 m개의 요소를 지우고 x를 추가
let arr = [1, 2, 3, 4, 5];
arr.splice(1, 3, 100, 200);
console.log(arr); //[1, 100, 200, 5]
let arr = [1, 2, 3];
arr.splice(1, 0, 100, 200);
console.log(arr); //[1, 100, 200, 2, 3]
arr.slice(n, m): n부터 m-1까지 반환
- m을 생략하면 n부터 배열 끝까지 반환
- 문자열에 파트에서 나온 slice와 같은 기능
let arr = [1, 2, 3, 4, 5];
arr.slice(1, 4); //[2, 3, 4];
let arr2 = arr.slice();
console.log(arr2); //[1, 2, 3, 4, 5] 출력
arr.concat(arr1, arr2, …): 합쳐서 새배열을 반환
let arr = [1, 2];
arr.concat( [3, 4] ); //[1, 2, 3, 4]
arr.concat( [3, 4], [5, 6] ); //[1, 2, 3, 4, 5, 6]
arr.concat( [3, 4], 5, 6 ); //[1, 2, 3, 4, 5, 6]
자바스크립트 기초 강의에서 배열의 반복은 for문이나 for…of를 사용
arr.forEach(func): 배열 반복, 함수를 인수로 받음
let users = [‘Baby’, ‘Angel’, ‘Noonsong’];
users.forEach((item, index, arr) => {
console.log(`${index+1}. ${item}`);
})
// 1. Baby
// 2. Angel
// 3. Noonsong→ item은 해당 요소 (Baby, Angel, Noonsong)
→ index는 배열의 인덱스 (0, 1, 2)
→ arr은 해당 배열 자체 (users)
→ 보통 첫번째와 두번째 인수만 사용, 세번째 인수 생략 가능
arr.indexOf(item, n): 배열의 인덱스 n부터 탐색을 시작, 진행 방향 →
arr. lastIndexOf (item, n): 배열 끝을 0으로 하여 n부터 탐색을 시작, 진행 방향 ←
- 찾아낸 item의 index 반환, 없으면 -1 반환
- n이 생략되면 indexOf는 처음부터 탐색 시작, lastIndexOf는 끝에서부터 탐색 시작
ex)
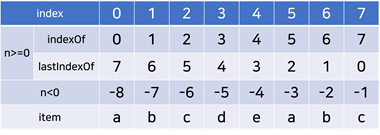
let arr = [‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘a’, ‘b’, ‘c’];
arr.indexOf(‘c’); //2
// → c의 위치는 index 2
arr.indexOf(‘c’, 3); //7
// → n>=3에서부터 탐색한 c의 위치는 index 7
arr.indexOf(‘c’, -4) //7
// → n>=-4에서부터 탐색한 c의 위치는 index 7
arr.lastIndexOf(‘c’); //7
//뒤에서부터 탐색한 c의 위치는 index 7
arr.lastIndexOf(‘c’, 6); //-1
// → n>=6에서부터 탐색한 c은 존재하지 않음, -1 반환
arr.indexOf(‘c’, -4) //2
// → n<=-4에서부터 탐색한 c의 위치는 index 2
arr.includes(item, n): 배열의 인덱스 n부터 탐색을 시작해서 item을 포함하는지 확인
- item을 포함하면 true, 그렇지 않으면 false 반환
- n을 생략하면 처음부터 탐색 시작
- n이 음수면 배열의 끝을 -1로 시작하여 배열 탐색
let arr = [1, 2, 3, 4, 5];
arr.includes(2); //true
arr.includes(8); //false
arr.includes(4, -3); //false
arr.find(func)
- 첫번째 true인 값만 반환하고 끝, 없으면 undefined를 반환
let arr = [1, 2, 3, 4, 5];
const result = arr.find((item) => {
return item % 2 === 0; //item이 짝수일 때 true
});
console.log(result); //2 출력
arr.findIndex(func)
- indexOf과 동일한 기능을 하지만 함수를 연결하여 좀 더 복잡한 연산이 가능
- 첫번째 true인 index 값만 반환하고 끝, 없으면 -1을 반환
let userList = [
{ name: ‘Baby’, age: 10 },
{ name: ‘Angel’, age: 27 },
{ name: ‘Noonsong’, age: 30 }
];
const result = userList.find((user) => {
if(user.age > 19) { return true; }
return false;
});
console.log(result); // {name: “Angel”, age: 27} 출력
const index = userList.findIndex((user) => {
if(user.age > 29) { return true; }
return false;
});
console.log(index); // 2 출력
arr.filter(func): 만족하는 모든 요소를 배열로 반환
let arr = [1, 2, 3, 4, 5];
const result = arr.filter((item) => {
return item % 2 === 0;
});
console.log(result); //[2, 4, 6] 출력
arr.reverse(): 배열을 역순으로 재정렬
let arr = [1, 2, 3, 4, 5];
arr.reverse(); //[5, 4, 3, 2, 1]
arr.map(func): 함수를 받아 특정 기능을 수행하고, 새로운 배열을 반환
let userList = [
{ name: ‘Baby’, age: 10 },
{ name: ‘Angel’, age: 27 },
{ name: ‘Noonsong’, age: 30 }
];
const newUserList= userList.map((user, index) => {
return Object.assign({}, user, {
isAdult: user.age > 19
});
});
console.log(newUserList);
// [
// {name: “Baby”, age: 10, isAdult: false},
// {name: “Angel”, age: 27, isAdult: true},
// {name: “Noonsong”, age: 30, isAdult: true}
// ]→ userList는 변경되지 않고 그대로
arr.join(): 배열의 모든 요소를 합해서 하나의 문자열로 반환
let arr = ["My", "name", "is", "Angel."];
console.log(arr.join()); //My, name, is, Angel. 출력
console.log(arr.join('')); //MynameisAngel. 출력
console.log(arr.join(' ')); //My name is Angel. 출력
console.log(arr.join('-')); //My-name-is-Angel. 출력
str.split(): 문자열을 지정한 구분자를 이용하여 여러 개의 문자열 배열로 반환
let str = "My name is Angel.";
const words = str.split(' ');
console.log(words); //["My", "name", "is", "Angel."]
const chars = str.split('');
console.log(chars); //["M", "y", " ", "n", "a", "m", "e", " ", "I", "s", " ", "A", "n", "g", "e", "l", "."]
const strCopy = str.split();
console.log(strCopy); //["My name is Angel."]
Array.isArray(): 전달받은 인자가 배열인지 아닌지 판별, 배열이면 true 아니면 false 반환
let user = {
name: 'Angel',
age: 30,
};
let userList = ["Baby", "Angel", "Noonsong"];
console.log(typeof user); //object
console.log(typeof userList); //object
console.log(Array.isArray(user)); //false
console.log(Array.isArray(userList)); //true
↓[코딩앙마] 자바스크립트 중급 강좌 링크
https://www.youtube.com/watch?v=pJzO6O-aWew
'Study > JavaScript' 카테고리의 다른 글
| [JavaScript] 중급 #9 - 구조 분해 할당 (Destructuring assignment) (0) | 2021.09.17 |
|---|---|
| [JavaScript] 중급 #8 - 배열 메소드2 (sort, reduce) (0) | 2021.09.13 |
| [JavaScript] 중급 #6 - 문자열 메소드 (String methods) (0) | 2021.09.06 |
| [JavaScript] 중급 #5 - 숫자, 수학 메소드 (Number, Math) (0) | 2021.09.06 |
| [JavaScript] 중급 #4 - 심볼(Symbol) (0) | 2021.09.06 |