Recursion with memorization – technique to improve the performance of a recursive program
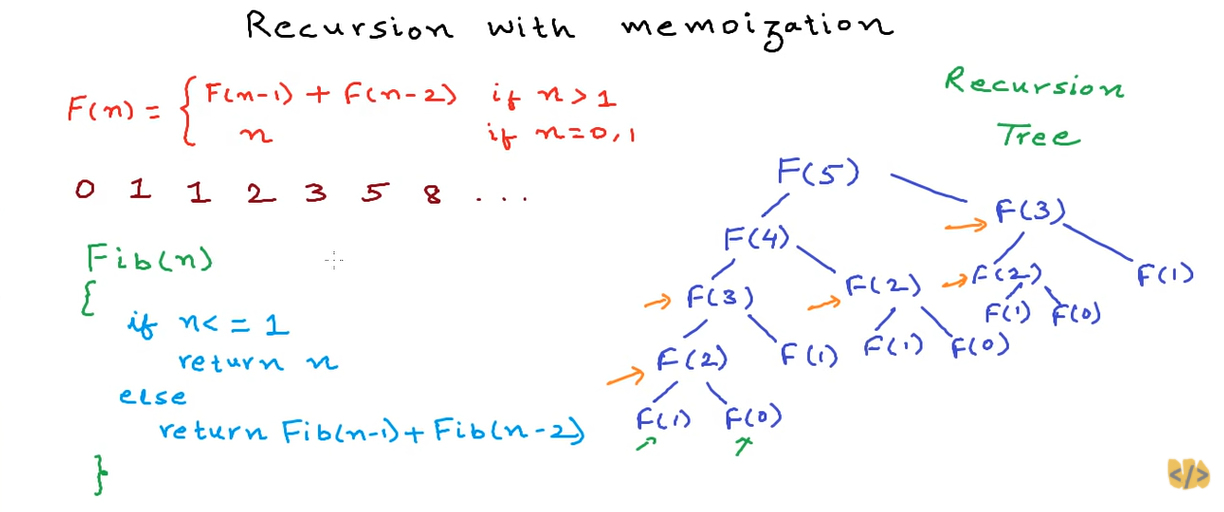
To avoid the recalculation of the same state or the same value, modify the function Fib(n) on the left.
When F(2) is calculated for the first time, save it in the memory so that it doesn’t have to be re-calculated.
And also any F(n), like F(3), F(4), and so on.
So if F(n) is in the memory, it doesn’t try to calculate, but simply return F(n).
Else, it tries to calculate F(n) by making recursive calls to calculate Fib(n-1) + Fib(n-2).
And save this F(n) in memory so that it doesn’t have to be re-calculated again.
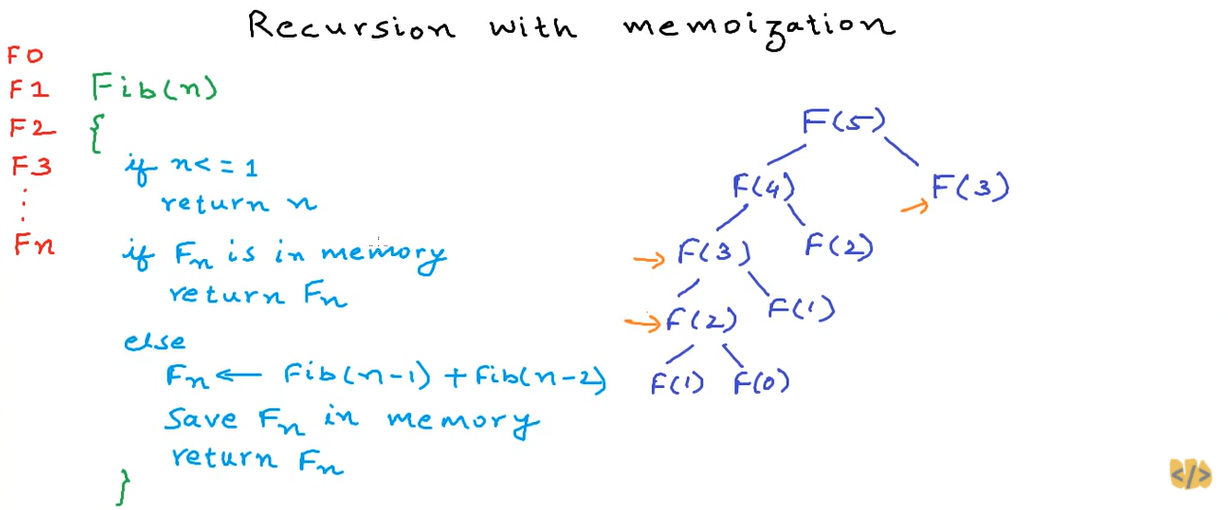
Now we can see the recursion tree with improvement.
When F(3) is being calculated, F(1) doesn’t have to be calculated again because it is already in the memory so simply returns the value.
It is same for F(4) and F(5) because F(2) and F(3) is already in the memory.
This implementation reduces the time complexity of this particular program.
previous code for Fibonacci
#include<iostream>
using namespace std;
int Fib(int n) {
if(n <= 1) {
return n;
}
return Fib(n-1) + F(n-2);
}
int main() {
int n;
cout<<"Give me an n: ";
cin>>n;
int result = Fib(n);
cout<<result;
}
improved code for Fibonacci
#include<iostream>
using namespace std;
int F[51];
int Fib(int n) {
if(n <= 1) {
return n;
}
if(F[n] != -1) {
return F[n];
}
F[n] = Fib(n-1) + F(n-2);
return F[n];
}
int main() {
for(int i=0; i<51; i++) {
F[i] = -1;
}
F[0]=0; F[1]=1;
int n;
cout<<"Give me an n: ";
cin>>n;
int result = Fib(n);
cout<<result;
}
So the recursion with memoization in this particular example is not as efficient as an iterative implementation in terms of memory, but it is as good as an iterative implementation in terms of time.
↓ 참고 사이트
https://www.youtube.com/watch?v=UxICsjrdlJA&list=PL2_aWCzGMAwLz3g66WrxFGSXvSsvyfzCO&index=5
'CS > Algorithm' 카테고리의 다른 글
| [Recursion] Exponentiation - Calculate Pow(x,n) using recursion (0) | 2021.09.17 |
|---|---|
| [Recursion] Fibonacci Sequence - Space Complexity analysis (0) | 2021.09.12 |
| [Recursion] Complexity analysis using factorial (0) | 2021.09.03 |
| [Recursion] Febonacci - Why recursion is not always good (0) | 2021.09.03 |
| [Recursion] Factorial (0) | 2021.09.03 |