Fibonacci Sequence - Anatomy of recursion and space complexity analysis
Let's try to analyze the space complexity of recursive implementation of Fibonacci sequence.
To understand and analyze the memory consumption, we need to understand how recursive program executes in the memory.

On the right, it is computers memory and these partitions in the memory are basically some units in which the memory is divided.
When a method is executing, it is currently in the memory.
So, all the local variables and the information about the method is already in the memory.
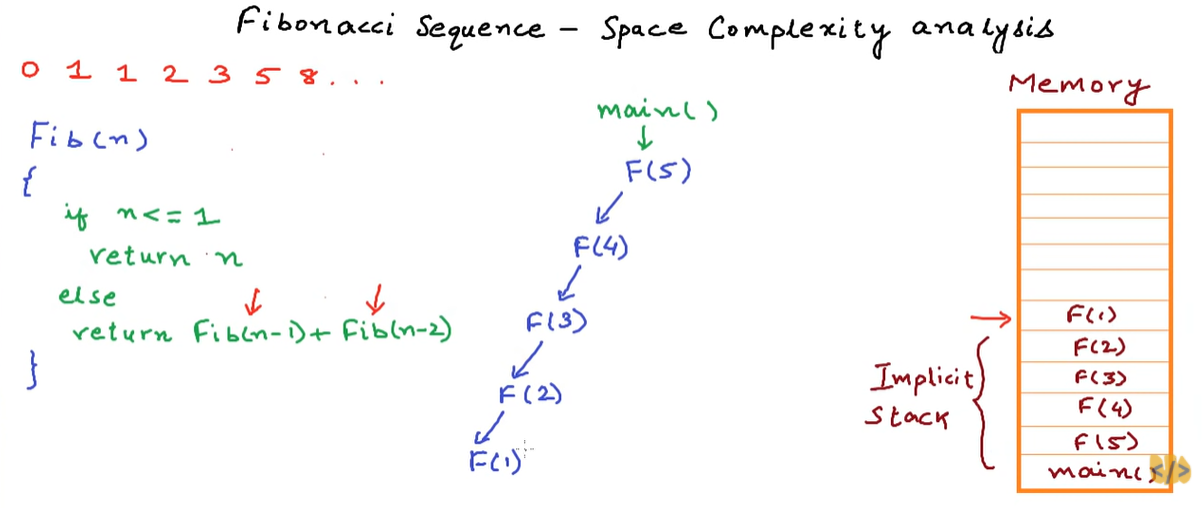
When this main method makes a call to another method F(5), computer saves the current state of execution of this particular method. It pauses main method and go ahead to calculate F(5).
Now, F(5) is executing and then F(5) makes a call to F(4), which is recursive call.
Next, F(4) is executing and the computer has saved the state of F(5) as well.
Keep going on until F(1), and F(1) will not make any further function call, or recursive call, but simply return 1.
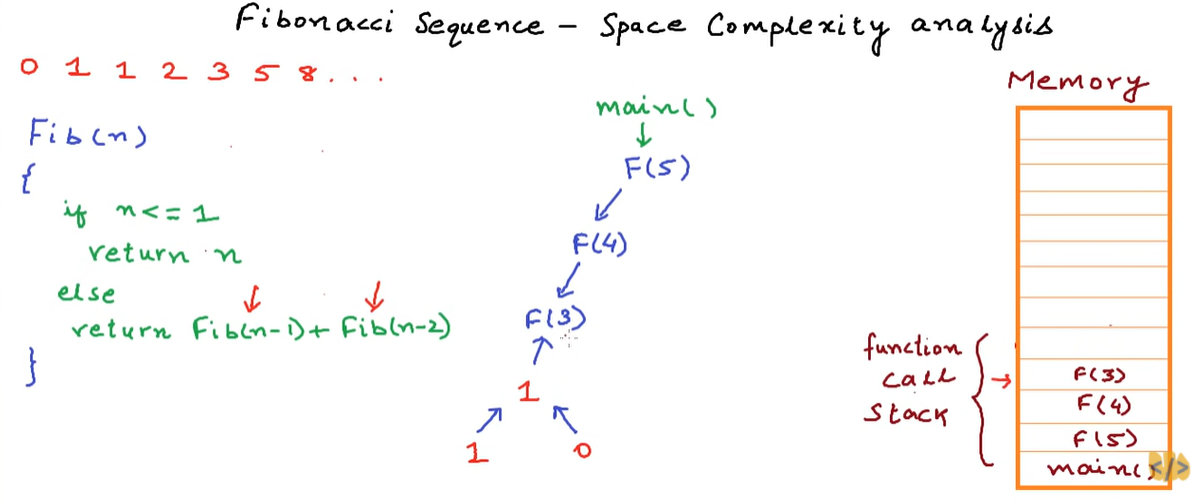
Now, F(1) has finished and it also gets popped from the memory and computer goes back to F(2).
F(2) at this stage makes another call to F(0), which simply returns 0 and finishes.
F(2) adds up these two values 1 and 0 and returns the sum 2 to F(3).
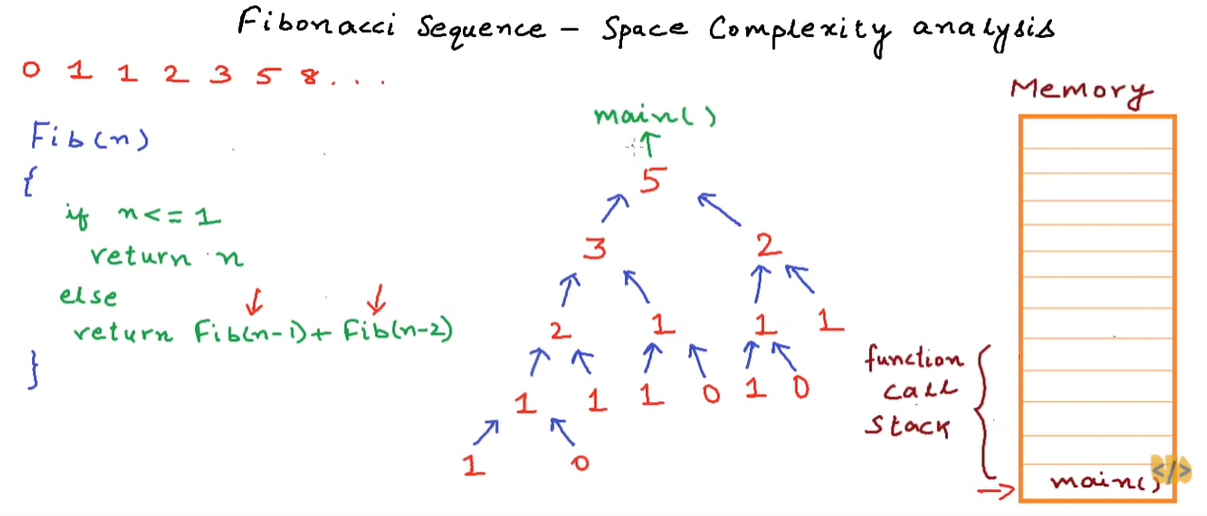
When F(5) sums up the two values, it returns to the main method which is its caller.
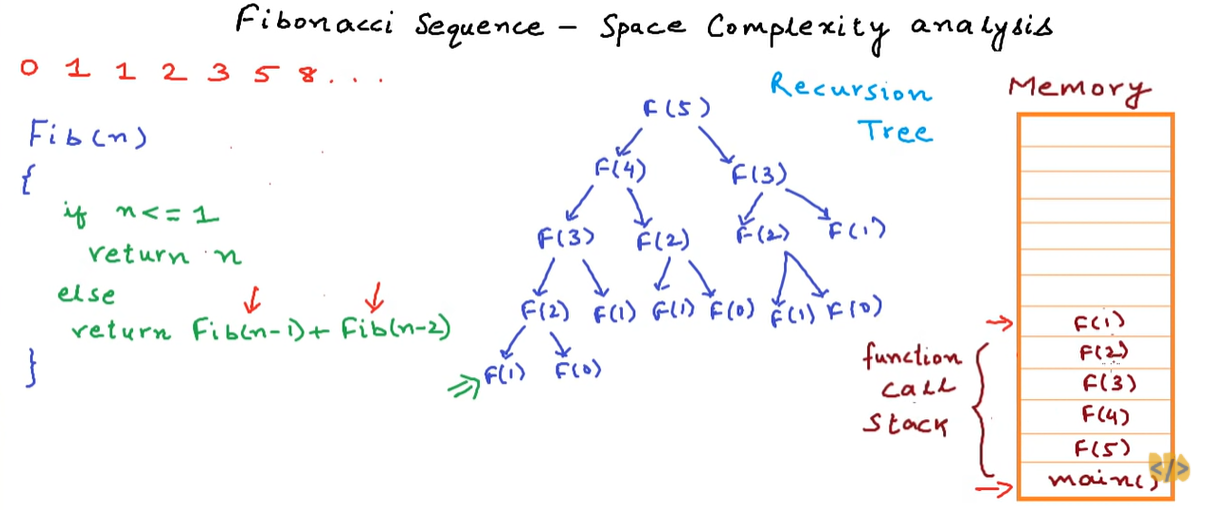
Now, the space consumed by this particular recursion was the memory that it consumed in the function call stack and the maximum growth of this call stack due to this particular recursion was when we were at the bottom-most node.
When F(1) was executing then all these states of F(5), F(4), F(3), F(2) were saved in the memory.
5 units of space were consumed in the memory and the call stack did not grow any larger than this.
The maximum space consumed by a recursive program is propotional to the maximum depth of this recursion tree.
And the maximum depth of recursion tree is defined as the length of the longest path in the tree.
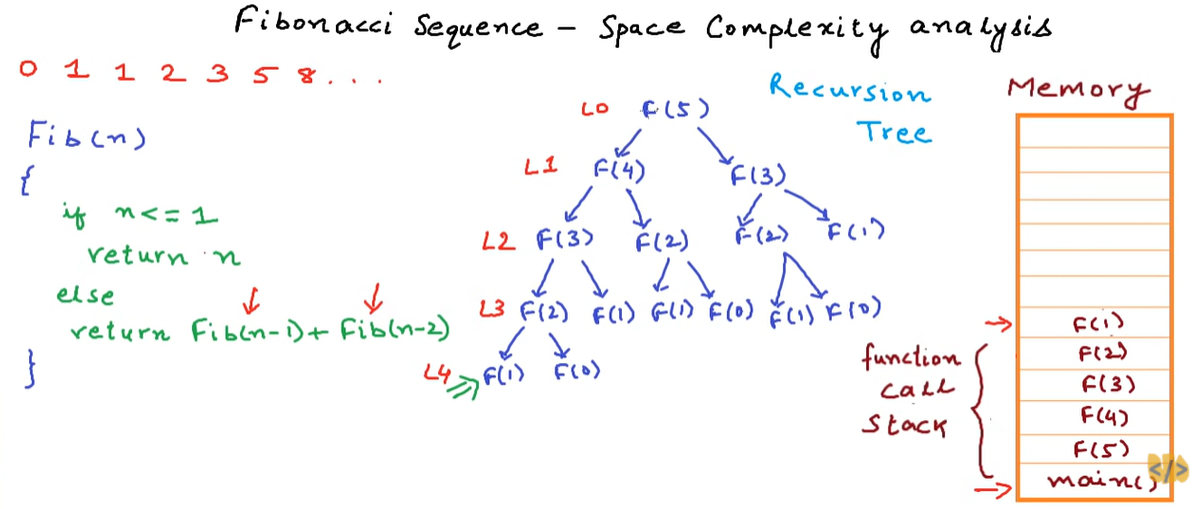
So if F(5) is Level0 in the tree and go down by one arrow, then F(4) is Level1, F(3) is Level2, F(2) is Level3, finally F(1) is Level4.
The maximum depth in this case is the path from Level0 to Level4, which is 4 units, and the number of function calls is 5 so the maximum memory consumed is 5 units.
If we would have called the function Fib(n) then the maximum depth of the recursion tree would have been n-1 units, and the maximum space taken would have been n units.
In this case space or memory consumption is proportional to n and we can also say that this is O(n) in terms of space complexity.
↓ 참고 사이트
https://www.youtube.com/watch?v=dxyYP3BSdcQ&list=PL2_aWCzGMAwLz3g66WrxFGSXvSsvyfzCO&index=6
'CS > Algorithm' 카테고리의 다른 글
| [Do it!] 3장. 검색 (Search) (0) | 2022.05.20 |
|---|---|
| [Recursion] Exponentiation - Calculate Pow(x,n) using recursion (0) | 2021.09.17 |
| [Recursion] Fibonacci Sequence - Recursion with Memoization (0) | 2021.09.12 |
| [Recursion] Complexity analysis using factorial (0) | 2021.09.03 |
| [Recursion] Febonacci - Why recursion is not always good (0) | 2021.09.03 |